先恭喜一下我自己煎熬了四個月終於退伍了XD。趁著退伍後的空閒時間趕快來補齊之前還沒寫完的SVM續集。😝
在上一篇白話文講解支持向量機(一) 線性SVM中我們學到了線性SVM的損失函數、目標函數,以及調整超參數C來決定決策線在訓練時對於資料點的靈敏程度。本篇我們將來介紹當資料不是單純可以線性分割時,非線性SVM是如何分類資料的。
以下是本篇講解的順序:
- 線性SVM(上一篇)
- 特性
- 損失函數
- 目標函數
- 目標函數中的正規化項
非線性SVM
我們就照上一篇的慣例先來舉個例子吧。假設我們今天得到的資料集他的資料分佈如下圖,有沒有什麼辦法可以將紅色方塊從圖中分類出來呢。
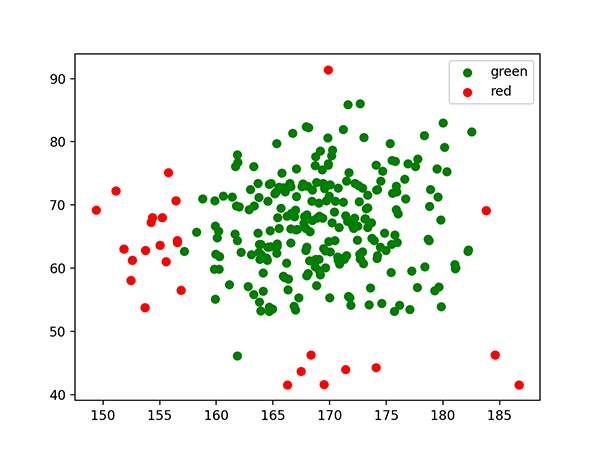
如果我們使用之前所學的線性SVM是辦不到的,因為這次的資料不像以往可以用一條直的決策線區隔出來。那怎麼辦呢,別擔心。大家如果有不經意看到一些職場修煉、職涯開導的書或文章時不是都會提到換位思考,要站在更高者的角度去思考局勢嗎。這個理論也適用我們現在的case:在低維度不能做到的事我們就拉到高維度去做。
特性
什麼叫「在低維度不能做到的事我們就拉到高維度去做」勒,請看下面的示意圖,我們首先把二維平面中的資料點送到三維空間中。
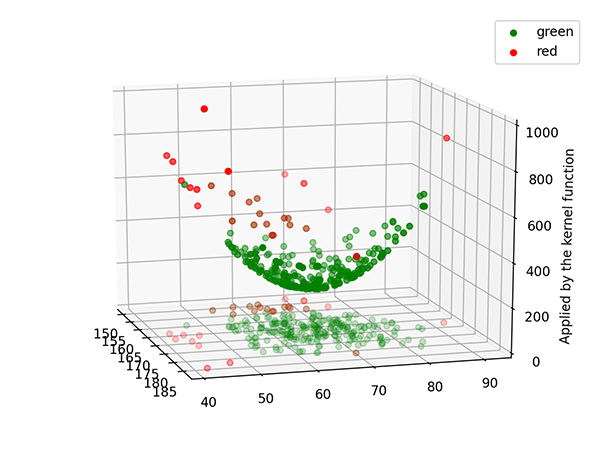
看似在二維平面中無法用決策線去切割的資料集,在三維空間中竟然輕而易舉的被一個超平面分割出來了。
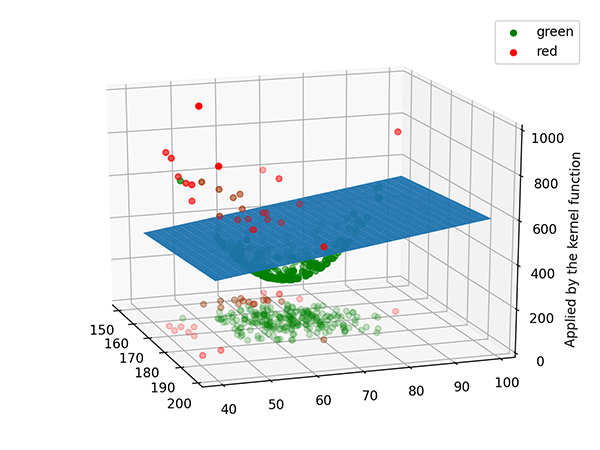
這就是要介紹的非線性SVM的最大的特性:在低維度不能做的分類,我們就到更高維度去做。聽起來是不是很酷炫呢,SVM就是因為採用了這個特性而造就成為經典。接下來我們來看看實際上這些資料點是怎麼被送到高維空間做分類的吧。
實際上的運作方式
其實剛剛上面講的概念 把低維度中的資料點送到高維度中,並且在高維空間中找出一個超平面去分割不同類別的資料 這句話雖然觀念是通的,但在實際運作上,非線性SVM是 把低維度中的資料點送到高維度中儲存起來,然後當非線性SVM要預測資料時,預測資料也會被送來高維度中與『每一組』訓練資料做運算。若運算結果大於0則被歸為一類,小於0即另一類。
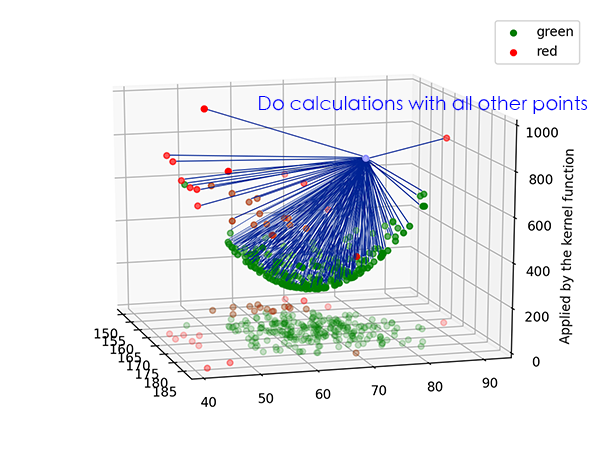
用上面這個新的角度去看非線性SVM對於等等談到怎麼預測、訓練以及訓練時會用到的kernel跟kernel trick超級有幫助。我也是卡在這邊很久很久最後當兵時某天忽然想通了。如果對我上面解釋的還是跨哞,可以參考一下英文維基百科解釋kernel method的地方,個人認為英文在描述事物時還是比較精準。好啦,如果到目前為止大家可以認同這個轉變後的新觀念了我們就可以繼續往下。
預測新資料
線性SVM在預測新資料時是將新的資料點代入決策線 θTx 計算結果,若運算結果大於0則被歸為一類,小於0即另一類。把決策線寫成 θTx 是我們上一篇為了篇幅而改寫的,原式為:
$$θ^Tx = θ_0x_0 + θ_1x_1 + θ_2x_2 \\ \textrm{let }x_0=1$$
非線性SVM在預測新資料時跟線性SVM十分相似,只不過這次換成了 θTf。以下是他的式子:
$$θ^Tf = θ_0f_0 + θ_1f_1 + θ_2f_2 + … + θ_mf_m$$
$$\textrm{let } f_0=1 \textrm{ 、} f_{(i)} = K(x_,t^{(i)}) \textrm{ where } i = 1…m$$
這個式子是由m+1項的和組成的,m是訓練資料的數量。除了第0項是常數項以外,剩餘的m項都是利用函數K把兩個低維度的資料送來高維度中做運算,之後再把得到的結果乘上前面該項的權重。而每一項要被送到高維度中做運算的東西正好就是我們要預測的資料x與第i筆訓練資料t(i)。
是不是可以體會到剛剛的新觀念 把低維度中的資料點送到高維度中儲存起來,然後當非線性SVM要預測資料時,預測資料也會被送來高維度中與『每一組』訓練資料做運算。若運算結果大於0則被歸為一類,小於0即另一類 了呢。這時,如果再回去用舊觀念來看的話也說得通唷:我們正在一個比原始資料更高的維度中尋找一個超平面 θTf 來分割資料。非線性SVM的特性是不是那麼的令人興奮呢。
Kernel
大家一路讀到這邊應該有發現我剛剛在前面賣了個關子。興奮一下就好,我們還是要來解釋一下那個函數K背後究竟是怎麼把兩個低維度的資料送到高維度中做運算的。
首先,函數K的真正名稱叫kernel function(核函數)。他在做的運算其實就是similarity measure(相似性度量)。當輸入kernel function的兩筆資料相似程度越大,輸出的值會越大,反之則越小。而且kernel function也不只有一種,像SVM中最常用的kernel function有polynomial kernel(多項式核)與RBF kernel(高斯核)。我們拿polynomial kernel來當範例拆解給大家看,自然看到式子大家就會明白kernel function是怎麼把兩個低維度的資料送到高維度中做similarity measure的。
這是polynomial kernel的數學式:
$$ K(x,y) = (x^Ty+c)^d $$
c是free parameter(自由參數)、d是維度,為了精簡化等等的演示,我們令c=1、d=2,然後把輸入向量x跟y的維度設為1就好,暫時把他們當純量在用。
$$ (xy+1)^2 = (xy+1) * (xy+1) \\ = (xy)^2 + 2xy + 1 \\ = (\sqrt{2}x, x^2, 1) ⋅ (\sqrt{2}y, y^2, 1)$$
數學化簡到這邊就結束了。雖然最後一行有點技巧故意拆成兩個向量的內積,不過如果單獨看那兩個向量,Do Re Mi So~,我們把輸入的x跟y各自從低維度中拉到高維度中了。不僅如此,他們最後做內積的動作其實就算是similarity measure呢。有沒有頓時感受到kernel的魔力所在呀。
Kernel Trick
$$K(x,y) = φ(x) ⋅ φ(x)$$
上面這個式子是kernel函數K利用函數φ把資料點送到更高維度中做內積,但實際上SVM不會真的這麼做。一來維度大大增加(剛剛舉的例子才令d=2,還可以無限制往更高維度去),二來好不容易在更高維空間中做完內積,最後得到了一個純量,想想這運算起來的cp值也太低了吧。因此,該輪到kernel trick出場來拯救我們了。
kernel trick聽其來很高深,但其實他就只是那個最一開始的kernel數學式而已,讓我們直接對兩個資料點做運算,而不用真的將兩個低維度的資料送到高維度中做內積,就這麼簡單。拿剛剛的polynomial kernel的例子來說(一樣令c=1、d=2,輸入向量x跟y的維度=1):
$$K(x,y) = (\sqrt{2}x, x^2, 1) ⋅ (\sqrt{2}y, y^2, 1)$$
我們不用真的這樣幹,只需要將x跟y代入最一開始的polynomial kernel數學式:
$$ K(x,y) = (x^Ty+c)^d = (xy+1)^2 $$
你們可以代數字進去驗算看看,計算這個數學式子相當於把兩個低維度的資料送到高維度中做內積,但是運算量是不是少很多呢。這就是講到非線性SVM時會常常聽到的kernel trick。
目標函數
在本篇的最後,我們把非線性SVM漏掉的目標函數也補上吧。
$$\min_{θ} C \sum_{i=1}^{m} [ y^{(i)} * loss_1(θ^Tf^{(i)}) + (1-y^{(i)}) * loss_0(θ^Tf^{(i)}) ] + \frac{1}{2} \sum_{j=1}^{n} θ_j^2$$
基本上跟線性SVM的目標函數非常類似,只差在中間多了一層kernel的作動,把 θTx(i) 換成了 θTf(i)。loss1與loss2依舊沿用線性SVM時的那兩個損失函數,使得非線性SVM在訓練時也是在想辦法最大化超平面θTf (或稱決策線、決策邊界)與支持向量的距離,只是這次的支持向量在更高的維度中了。
超參數C仍然控制著前半部份的分類損失與後半部份正規化項的比例,最終影響訓練出來的超平面究竟要傾向盡可能地將所有資料點正確分類(低偏差高變異),還是允許一些被錯誤分類的離群值但最大化超平面兩邊與支持向量的邊界距離(高偏差低變異)。比如剛剛在資料在原始維度中就包含了離群值:
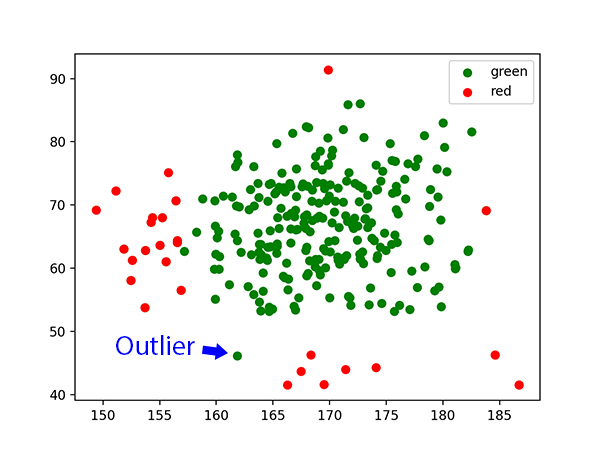
當C設得較小時,非線性SVM在高維空間會對被錯誤分類的資料點比較寬容。
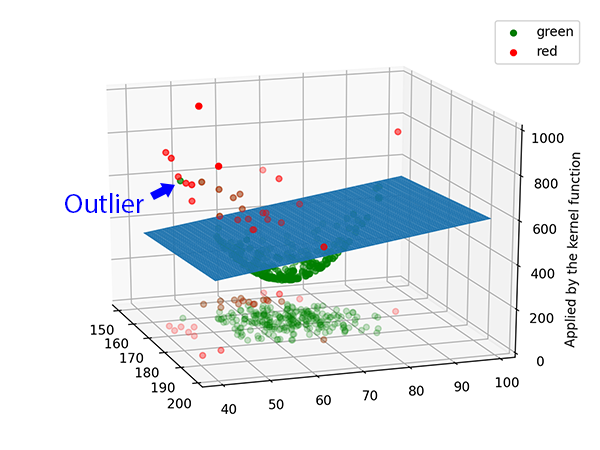
除了這些外,使用不同的kernel function也會有相對應可以調整的超參數,例如polynomial kernel在scikit-learn套件中就默認超參數d(維度)是3。
後記
SVM是一個很優秀很經典的機器學習演算法。我在自學SVM時不外乎跟大家一樣就是學到那三個重要的特性 想辦法最大化決策線(或超平面)的邊界距離、藉由kernel把低維度中的資料點送到高維度中運算他們的關係、其實利用kernel trick就可以不用真的將資料送去更高的維度做運算。但我僅此於死背他們的特性而已,就連在高維度中運算他們的關係到底跟做分類有什麼關係都不清楚。相信很多也是自學SVM的人看了很多網路文章的解釋應該很有同感吧。
直到我在當兵時完整的把SVM重新想過了一邊後突然想通了,因此希望可以打鐵趁熱寫一篇最白話文的方式講解SVM,把這幾個觀念釐清後串在一起。希望可以幫助到更多跟我一樣每個觀念都懂,但就是沒辦法將所有觀念融入在一起的人。
因為這兩篇都是focus在用最直觀的方式表達觀念居多,所以在有些公式上寫得不太嚴謹請見諒:P 。如果看完後還是有不懂的問題歡迎在下面留言,我會盡我的能力回答你的。
您好~
您真的是寫得非常好。
另外,
想請問您說Kernel trick的第一行方程式,
是不是其中一個函數φ的變數應該是y呢?
也就是一個變數是x一個變數是y
謝謝您抽空回應
謝謝