大學畢業後7月正式入伍登入了國軍online。在軍中由於有太多的時間可以發呆思考人生,所以想說利用這些時間把一些機器學習的模型在頭腦裡跑過一遍。SVM在機器學習領域裡算是一個滿經典的演算法,因此值得趁記憶猶新時花些篇幅記錄一下,希望可以以我自己比較白話的理解方式介紹SVM。
我將以下面的順序講解SVM,先讓大家有個大致的概念:
- 非線性SVM(下一篇)
- 特性
- 實際上的運作方式
- 預測新資料
- Kernel
- Kernel Trick
- 目標函數
本篇會先從線性SVM開始講起,如何使用一條直線、一個平面或是在更高維度的任何線性函數來達成二元分類。除了線性的SVM以外,也有非線性SVM。不過我覺得線性SVM跟非線性SVM還是要明確分開來講比較好,不然像我在自學的時候就把這這兩個混在一起看,導致在kernel的觀念那邊卡關很久。
因此下一篇我們才會進入非線性SVM,假設資料不是單純可以線性分割時,SVM可以怎麼變化達成非線性的切割,進而帶到非線性SVM使用的kernel概念、以及實際上電腦在訓練時都會採用kernel trick優化減少運算量。
線性SVM
我們就拿一個簡單的二元分類問題來切入SVM吧。
請問各位覺得哪條決策線才是正確的切法,分割出藍色圓圈與紅色方塊這兩個類別的資料呢?
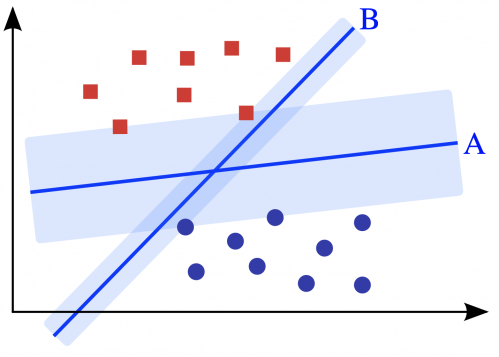
答案是沒有標準答案,只要所選擇的決策線能夠將資料成功切出在線的兩端,這些決策線對於這群資料來說表現得都一樣好,因此上面這個問題的答案除了A、B那兩條外還有無限種可能的決策線。
但是實際上,大家應該都會覺得上圖決策線A比決策線B來得佳吧。假設今天又多了一個綠色三角形(如下圖),我們人類憑直覺會把綠色三角形歸類在紅色方塊那類,決策線A也會這們認為。但如果依照決策線B的分類方式,綠色三角形應該跟藍色圓圈才是同一類呢。
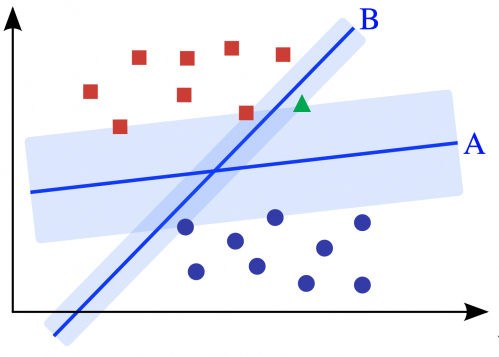
會發生決策線B的這種結果,將綠色三角形跟藍色圓圈分在同一類的最大原因就是因為決策線B離資料點太近了。因此,我們會希望除了能找到一條決策線能將資料成功切出在線的兩端,這條決策線也必需能離資料點越遠越好。
特性
SVM也會認為決策線A是這群資料中的最佳決策線。那SVM是怎麼找到決策線A的呢,首先SVM會計算出在不同資料類別之間最前線的資料點,我們稱為支持向量(support vectors),如下圖中綠色框起來的部份。接下來SVM會在這些支持向量之間找決策線,使決策線與支持向量們有著最大的邊界距離。這個與支持向量們有著最大邊界距離的決策線即為SVM最終找到的解。大家應該不難體會這就是SVM(支持向量機)分類演算法名字中SV(支持向量)的由來。
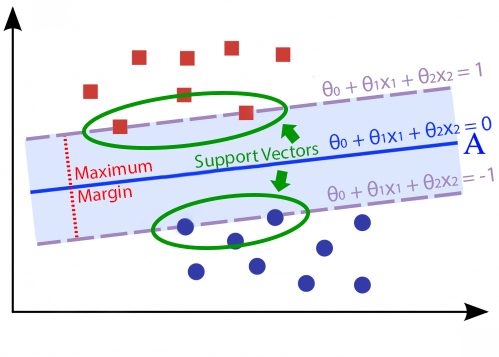
到目前為止,我們已經以最直觀的方式理解SVM的概念了。我們接著要來看看SVM的數學運作原理,看看SVM是如何計算訓練過程中的損失的,以及他在訓練時最終要優化的目標函數。
損失函數
我們都知道當一個點代入決策線方程式時,如果該點恰巧座落於決策線上則會得到0;當該點位於決策線的其中一側時,代入決策線方程式則會得到大於0的值、另一側則是小於0。隨著該點離決策線越來越遠而去,該點代入決策線方程式所產生的值也會往正負無限大趨近。拿決策線做預測時也是這樣的概念,當一個點代入決策線方程式時得到的值大於0,我們會將他歸在同一類;反之如果值小於0則歸在另一類。
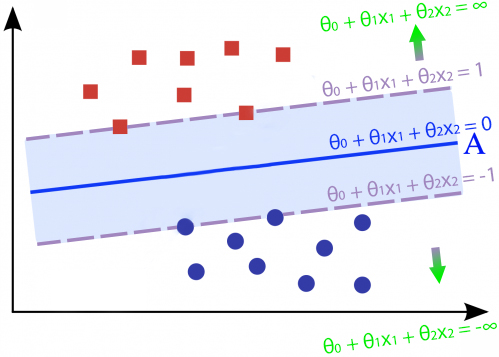
了解這樣的特性後,我們就可以來定義SVM的損失函數了。SVM在訓練時為了最大化決策線與支持向量的距離,不只希望點紅色方塊類別的資料點位於決策線的其中一側,還希望代入決策線方程式會得到大於1的值(最好離決策線越遠越好)。因此對於紅色方塊類別的資料點的損失函數可以寫成:
$$loss_1(θ^Tx) = max(0, (1-θ^Tx))$$
其中我們把決策線改寫成比較短的方式表示:
$$θ^Tx = θ_0x_0 +θ_1x_1 + θ_2x_2 \\ \textrm{let }x_0=1$$
(往後我們都用這樣的方式表達決策線)
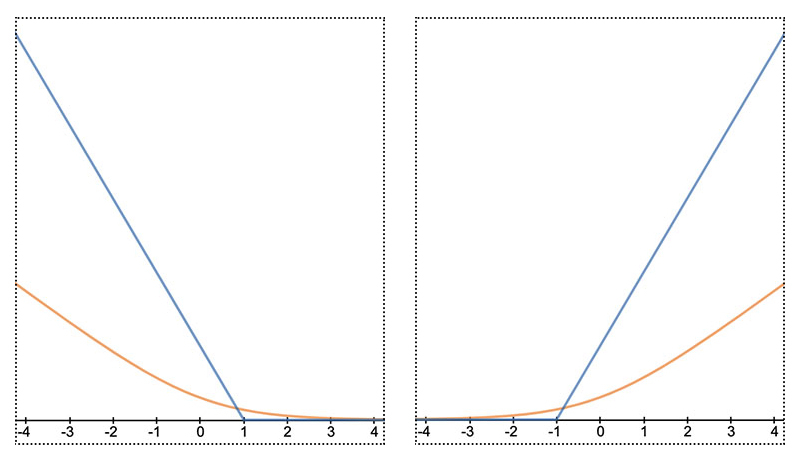
函數圖形如下面左圖的藍色部份。這個函數在意義上是在說:如果將紅色方塊類別的資料點帶入決策線方程式出來的值小於1(離決策線太近),那就會在訓練過程中產生損失,且損失會根據遠近而變大。
另一方面,SVM也不只希望藍色圓圈資料點位於決策線的另一側就好,還希望代入決策線方程式會得到小於-1的值(也是能離決策線多遠就多遠)。因此對於藍色圓圈類別的資料點的損失函數可以寫成:
$$loss_0(θ^Tx) = max(0, (1+θ^Tx))$$
函數圖形如下面右圖的藍色部份。這個函數在意義上也是在說:如果將藍色圓圈類別的資料點帶入決策線方程式出來的值大於-1(離決策線太近),那就會在訓練過程中產生損失,且損失也是會根據遠近而變大。
看到這邊大家應該都有些feeling了,數學上SVM是如何對決策線與支持向量靠太近的狀況去計算損失。有了損失後,只要開始調整決策線參數θ,找到一組能讓損失最小的θ,那以這組參數組成的線就是SVM最終目標要找的決策線了。
目標函數
我們先把上面這長長的一句話翻譯成數學式子來表示:
$$\min_{θ} \sum_{i=1}^{m} [ y^{(i)} * loss_1(θ^Tx^{(i)}) + (1-y^{(i)}) * loss_0(θ^Tx^{(i)}) ] $$
m是全部訓練資料的總筆數、y是訓練資料的類別(1或0兩類),我們要找出一組θ來minimize(最小化)所有訓練資料在loss1與loss0的和。至於該筆訓練資料應該適用loss1還是loss0呢,就交由前面的y或(1-y)來判斷。
如果該筆資料是被標記在類別1,後面(1-y)會讓loss0不作用,因此類別1的資料就只會計算loss1的損失;反之如果該筆資料是被標記在類別0,前面loss1不會作用,因此類別0的資料只會計算loss0的損失。
到目前為止好像聽起來都還不錯吧,但現實中的資料總是沒那麼美好,比如說今天資料中出現了離群值。
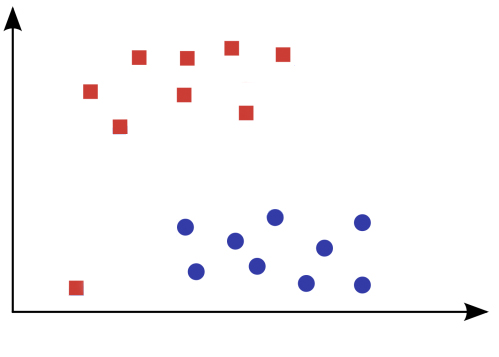
如果將帶有離群值的資料拿給SVM訓練的話,SVM為了最小化剛剛的目標函數,會想辦法找出一條決策線,使這條決策線切出不同類別的資料點在他的左右兩側,並且決策線也不能太靠近左右兩側的支持向量,最終又會訓練出如本篇開頭例子的決策線B。SVM好爛喔,這演算法一點都不經典啊。。。
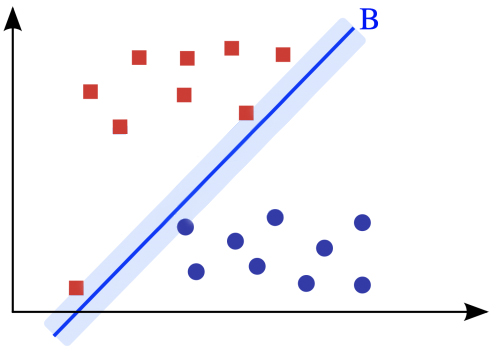
別急,SVM當然也有考慮到現實資料中的離群值與不是所有資料都是線性可分的狀況會發生,因此SVM在目標函數中還加入了正規化項(regularization term):
$$\sum_{j=1}^{n} θ_j^2$$
(n是決策線中可訓練的參數數量)
然後把正規化項加至目標函數的後半部份,整個SVM的目標函數最終會長這樣:
$$\min_{θ} C \sum_{i=1}^{m} [ y^{(i)} * loss_1(θ^Tx^{(i)}) + (1-y^{(i)}) * loss_0(θ^Tx^{(i)}) ] + \frac{1}{2} \sum_{j=1}^{n} θ_j^2$$
在最終目標函數中的C是在訓練SVM時可以調整的超參數(hyperparameter),拿來控制前半部份的分類損失與後半部份正規化項的比例用的。像是在scikit-learn套件中的線性SVM分類器,超參數C的預設值是1.0。
目標函數中的正規化項
在本篇的最後,我們來解釋一下為什麼加入了正規化項的SVM就有抗離群值的能力,這樣整篇介紹線性SVM才算得上完整。我們先從兩條平行線的距離公式開始說起:
$$d=\frac{|C_1-C_2|}{\sqrt {A^2+B^2}}$$
公式中使用的兩條直線:
$$Ax+By=C_1 \textrm{ 、} Ax+By=C_2$$
相信大家在高中的數學課本上都有見過這個公式,不會太陌生。接著我們把距離公式套在兩條與決策線平行且經過兩個類別的支持向量的最大邊界線上,準備來算出兩個最大邊界線之間的距離。
兩條最大邊界線(整理成上面的形式):
$$θ_1x_1 + θ_2x_2 = (-θ_0 + 1) \textrm{ 、} θ_1x_1 + θ_2x_2 = (-θ_0 -1)$$
代入公式:
$$d=\frac{|(-θ_0 + 1)-(-θ_0 - 1)|}{\sqrt {θ_0^2+θ_1^2}}=\frac{2}{||θ||}$$
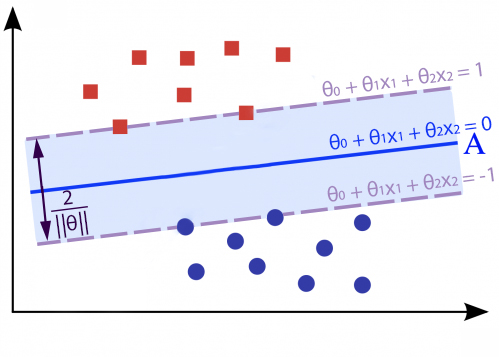
我們要讓兩個最大邊界線之間的距離越大,就必需讓分母的||θ||越小。而這正是在目標函數後半部加入正規化項的用意。
$$\min_{θ} C \sum_{i=1}^{m} [ y^{(i)} * loss_1(θ^Tx^{(i)}) + (1-y^{(i)}) * loss_0(θ^Tx^{(i)}) ] + \frac{1}{2} \sum_{j=1}^{n} θ_j^2$$
這跟抗離群值有什麼關係。有的,還記得我們有個超參數C可以控制目標函數前半部份的分類損失與後半部份正規化項的比例對吧。
- 當
C越大,SVM在訓練時越重視前半部份的分類損失,因此會想盡辦法找出一條決策線將不同類別的資料點切在自己線的左右兩測(如決策線B)。同時,自己這條決策線要離左右兩側的支持向量越遠越好(置中的概念),否則損失會很大。 -
當
C越小,SVM在訓練時越重視後半部份的正規化項,前面的分類損失就漸漸變得不那麼重要(能接受一些資料點例如離群值被分錯類)。SVM開始傾向找出一條決策線,使與決策線平行的兩個最大邊界線之間的距離越大越好(如決策線A)。
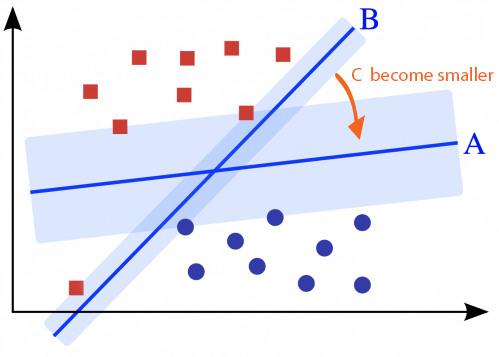
總而言之,在訓練時適當的調整超參數C可以控制希望決策線要偏向C較大時的低偏差高變異(low bias high variance)還是C較小的高偏差低變異(high bias low variance)。是不是豁然開朗、感覺到SVM既簡單又強大了呢。
下一篇我們要介紹非線性的SVM,當資料不是單純可以線性分割時SVM該如何分類資料。