以公開的方式交換資訊生成對稱式金鑰

最近讀的密碼學的書裡面介紹了Diffie–Hellman Key Exchange，覺得很有趣，紀錄一下

 

使用情節

小明想與小華想利用對稱式加密建立加密連線

可是不管是任何一方先產生金鑰再傳送給另外一方都有被第三方監聽的風險

這時，Diffie–Hellman Key Exchange就派上用場了

Diffie–Hellman Key Exchange用於當溝通的雙方處於不安全連線(被第三方監聽)下

仍能交換資訊生成對稱式金鑰建立加密連線

 

密鑰生成步驟

藍色表示可以公開被第三方聽到的資訊
灰色表示不可以公開被第三方聽到的資訊
橘色表示兩人運算完後產生的金鑰

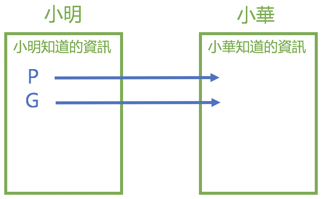
1. 小明隨機把兩個質數P、G傳送給小華
   質數P、G可以用明碼傳送，被第三方知道了也沒關係
   

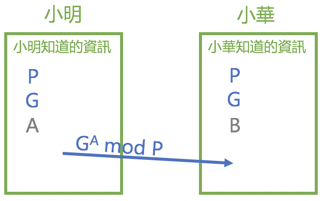
2. 小明額外再生成一個隨機數A
   這個隨機數A就不能讓任何人知道，連小華也不必知道
   

3. 小華生成一個隨機數B
   這個隨機數B也不能讓任何人知道，連小明也是
   

4. 小明將 (G^A mod P) 的值計算出來傳送給小華
   

5. 小華將 (G^B mod P) 的值計算出來傳送給小明
   

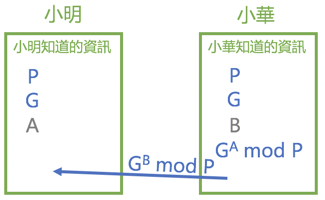
小明現在有P、G、A、(G^B mod P) 這四個值，而小華現在有P、G、B、(G^A mod P) 這四個值

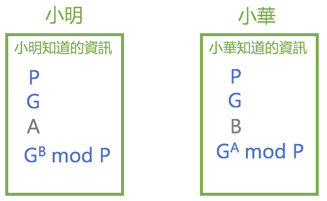
6. 小明把 (G^B mod P)^A mod P 的值計算出來
   (G^B mod P)^A mod P 可以簡化成 (G^BA mod P)

7. 同樣地，小華把 (G^A mod P)^B mod P 的值計算出來
   (G^A mod P)^B mod P 可以簡化成 (G^AB mod P)

到這裡可以發現，小明與小華計算出來的值都一樣是 (G^AB mod P)

(G^AB mod P) 也就是他們兩個之間產出拿來加密對話的對稱式金鑰

 

代數字示範

因為是示範，所以拿比較短的數字，實際上P、Ａ、B必須夠大才安全

1. 小明把兩個質數P、G傳送給小華
   質數P = 23
   質數G = 5

2. 小明額外再生成一個隨機數A，A = 6

3. 小華生成一個隨機數B，B = 15

4. 小明將 (G^A mod P) 的值計算出來傳送給小華
   (5⁶ mod 23) = 8

5. 小華將 (G^B mod P) 的值計算出來傳送給小明
   (5¹⁵ mod 23) = 19

6. 小明把 (G^B mod P)^A mod P 的值計算出來
   (5¹⁵ mod 23)⁶ mod 23 = 19⁶ mod 23 = 2

7. 同樣地，小華把 (G^A mod P)^B mod P 的值計算出來
   (5⁶ mod 23)¹⁵ mod 23 = 8¹⁵ mod 23 = 2

最終小明與小華都得到了共同數值 2 成為雙方拿來加密對話的對稱式金鑰

 

第三方能透過監聽算出金鑰嗎

假如第三方小美從頭到尾完整擷取了他們使用Diffie–Hellman Key Exchange的過程

小美共可以獲得P、G、(G^A mod P)、(G^B mod P) 這四個值

但是只要P、Ａ、B夠大，根據離散對數問題，是沒辦法輕易找出 (G^AB mod P) 的

 

弱點

使用Diffie–Hellman Key Exchange產生金鑰雖然可以防止第三方監聽

但如果遇到中間人攻擊那就沒輒了

小美若介入了小明與小華的對話

當小明將 (G^A mod P) 傳送給小華時把訊息給攔截

並假冒成小明傳送 (G^C mod P) 給小華
(C是小美自己產生的隨機數，加上公開的P與G即可產生 (G^C mod P) )

依樣畫葫蘆，當小華將 (G^B mod P) 傳送給小明時把訊息攔截

並假冒成小華傳送 (G^D mod P) 給小明
(D是小美自己產生的隨機數，加上公開的P與G即可產生 (G^D mod P) )

如此一來，小美即成為擁有金鑰的中間人

往後可以神不知鬼不覺的把加密訊息用現有的P、G、C、D給解密了